Veröffentlicht am 6.07.2020 von Tobias Moxter

Neben den unmittelbaren Arbeiten an der Entwicklung unseres hybriden Motorseglers hat sich das Team der FVA 30 im letzten Monat auch der Veröffentlichung neuer Eindrücke aus den Auslegungsprozessen gewidmet. Für die 79. SAWE International Conference on Mass Properties Engineering, die dieses Jahr in Hamburg sattfinden sollte, haben wir ein Paper über die Fortpflanzung von Unsicherheiten in den Massenannahmen in der Auslegung von Motorseglern eingereicht. Auf diesem Weg wollen wir unsere Erfahrungen zu einem sehr dynamischen Prozess in den frühen Phasen der Prototypenentwicklung teilen, in dem die letztendlichen Massen und Positionen der Bauteile und Komponenten noch große Unbekannte sind.
In dem Wettbewerb des besten Studentpapers gewannen wir hierbei den zweiten Platz. An dieser Stelle, herzlichen Glückwunsch an das gesamte Team!
Der Ausgangspunkt dieser Überlegung war die Beobachtung, dass wir im Zweifel in der Regel die konservative Abschätzung wählen, um bei Abweichungen immer auf der sicheren Seite zu liegen. Über die vielen verschiedenen Komponenten hinweg entsteht dabei aber unweigerlich ein derart pessimistisches Bild, dass es nicht mehr rational ist in jedem Fall konsequent vom höchsten Gewicht und der ungünstigsten Position auszugehen. Auf diesem Weg entstand nun ein Tool, das ausgehend von dem Spielraum der Massen und Positionen eine resultierende Wahrscheinlichkeitsverteilung für die Gesamtmasse und den Gesamtmassenschwerpunkt des Motorseglers erstellt. Wie erwartet stellt sich die Wahrscheinlichkeit der pessimistischsten Konfiguration als verschwindend gering heraus, sodass es nicht sinnvoll ist, an dieser Annahme festzuhalten.
Als Ausgangspunkt wählten wir für die jeweiligen Massen und Positionen der unbestimmten Komponenten eine eigene Wahrscheinlichkeitsverteilung. Für gewöhnlich kann die Unsicherheit der Werte zum Beispiel auch durch die Angabe eines Rahmens oder durch einen Erwartungswert und eine zugehörige Standartabweichung beschrieben werden. Wir wählten stattdessen Verteilungen, die entweder einer Reihe von disktreten Wahrscheinlichkeitswerten, einer Gauss-Verteilung, einer „students’s t-Verteilung“, oder einer Gleichverteilung entspricht. Diese Verteilungen wurden gewählt je nachdem welche Angaben über die Unsicherheiten getroffen werden konnten, bzw. je nachdem welche Information uns zur Verfügung stand.
Die Fortpflanzung der Unsicherheiten beim Zusammenstellen des Gesamtkonzepts wurde dann mittels Monte Carlo Methoden gehandhabt und in Python implementiert. Wie in Abb. 2 zu sehen, erhielten wir so zuletzt die finalen Verteilungen. Wie nach dem Gesetzt der großen Zahlen erwartet, nähern sich diese zunehmend der Normalverteilung an.

Abb. 1: Wahrscheinlichkeitsverteilungen für eine Auswahl von Komponenten.
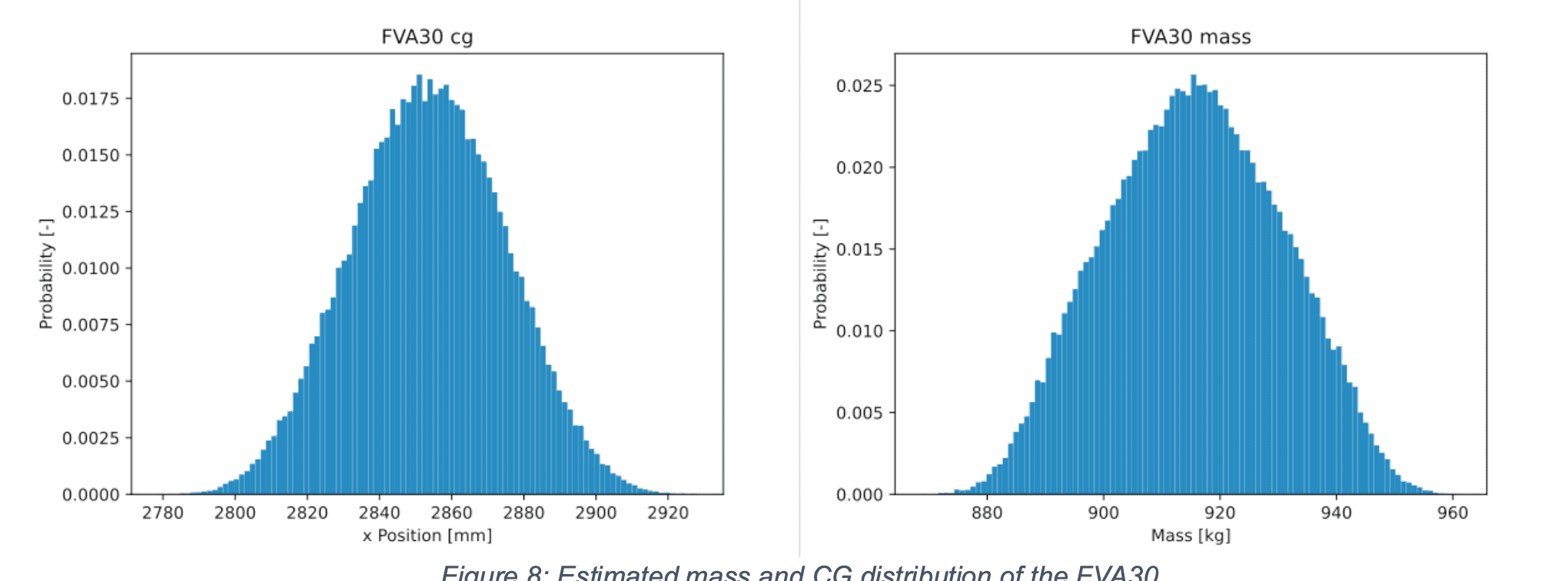
Abb. 2: Resultierende Verteilungen für den Schwerpunkt in x/längs Richtung (links) und die Gesamtmasse (rechts)